A Walter számok halmaza

Ajánlom minden olyan ismerősöm figyelmébe, aki azt hiszi, hogy a gyök kettő nem is igazi, az \(i\) pedig egyáltalán nem létezik.

Szóval kezdett elegem lenni abból, hogy egyesek néhány sör után elkezdik támadni a számukra ismeretlen matematikai fogalmak sokaságát azzal az érvvel, hogy olyan nincs is. Igen, a gonosz matematikusok kitalálnak mindenféléket csak azért, hogy ezzel is bosszantsák a köznépet.

Hosszas gondolkodás után arra jutottam, hogy az emberek legnagyobb része úgy néz minden matematikai fogalomra, hogy azt próbálja beleerőltetni a számára ismeretes fogalmak rendszerébe, és ha nem megy, akkor az új fogalom minden bizonnyal lehetetlen.

Vegyük például a \(\sqrt{2}\)-t. Sok ember számára az irracionális számok egyszerűen nem léteznek (\(\mathbb{I} = \varnothing\)). A számok összessége tehát a racionális számok (\(\mathbb{Q}\)) halmazára korlátozódik. Ha egy ilyen személynek azt mondjuk:

— Képzeld Feri1, \(x^2=2\) .

Feri ezt így értelmezi:

— Képzeld Feri, \(x^2=2 \land x \in \mathbb{Q}\) .

És így válaszol:

— De hát Jola2! \(x \in \varnothing\) !

A racionális számokkal (\(\mathbb{Q}\)) már többen ki vannak békülve, az egész számokat (\(\mathbb{Z}\)) pedig mindenki komázza. Pedig ha ugyanezt megcsináljuk egy gyerekkel:

— Szia Peti! Hallottad? \(x = 1-2\) !

Peti fejében:

— Szia Peti! Hallottad? \(x = 1-2 \land x \in \mathbb{N}\) !

— De Attila, hiszen \(x \in \varnothing\) !

És aztán megkérdezzük Ferit,

— Feri, mit szólsz Peti válaszához?

— Ne bántsd már! Peti alig múlt kettő, majd ha nagyobb lesz, megérti.

Pedig Peti és Feri ugyanazt a hibát követik el: a kérdést úgy értelmezik, ahogy az az ismereteiknek megfelel. És sok egyetemet végzett ismerősöm is ugyanúgy belesétál ebbe.

Ezért szeretném kihangsúlyozni minden kedves olvasó számára, hogy amikor azt mondja valaki, hogy \(x^2 = -1\), azt nem úgy érti, hogy \(x^2 = -1 \land x \in \mathbb{R}\), mert hát \(x = i\), és ezzel meg is ismertük a komplex számok halmazát:

\[\mathbb{C} = \{z \colon z = (ai+b) \land a, b \in \mathbb{R} \land i^2 = -1\}\]

Itt sem kell megállni, hogy “jól van, több már úgysincs”, mert én meg azt mondom:

\[x^2 = 1 \land x \notin \{i^n \colon n \in \mathbb{R} \land i^2 = -1\}\]

Nyilvánvaló, hogy \(x \notin \mathbb{C}\). Ez viszont nem jelenti azt, hogy \(x \in \varnothing\), mert nem adtam meg semmilyen “fölső határt” \(x\)-re. Sőt, a fönti egyenlőségrendszernek számtalan megoldása van, csakhogy egyik sem komplex. (A kortárs matematikában a fönti képlet megoldását \(j\)-vel szokták jelölni.)

A számtalan megoldás közül csak egyet említenék meg:

\(x =\)

Ezzel definiáljuk az ún. Walter-féle számokat:

\(\mathbb{W} = \{w \colon w = (a\) \(+b) \land a, b \in \mathbb{C} \land\) \(^2 = 1 \land\) \(\notin \{i^n \colon n \in \mathbb{R} \land i^2 = -1\}\}\)

A \(\mathbb{W}\) halmazt a többi számhoz viszonyítva az alábbi Venn-diagrammal szemléltetem:

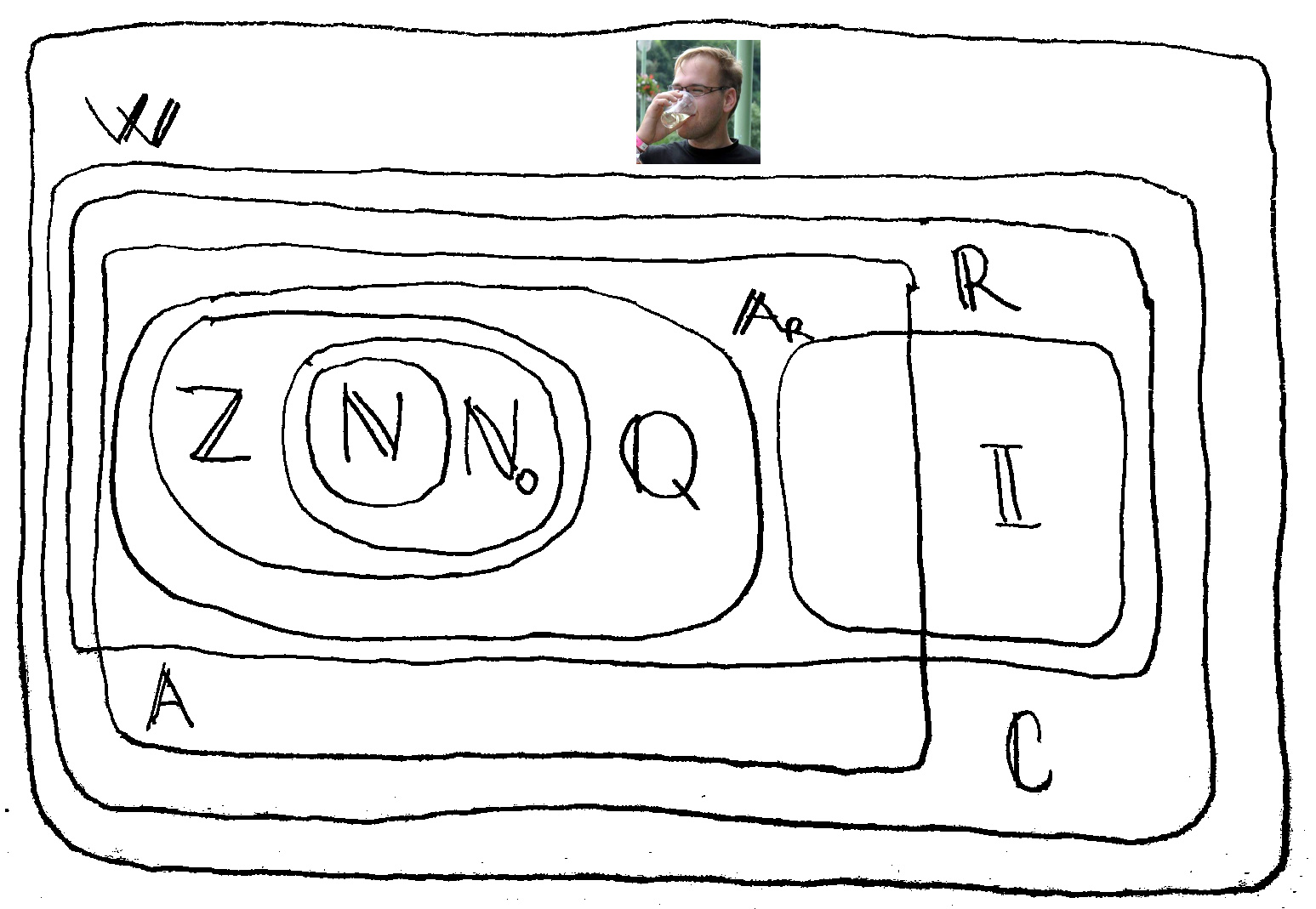
W halmaz

Melyben:

A Walter számok halmazára érvényesek a következők:

  • A \(\mathbb{W}\) halmaz számossága \(\aleph_2\) (lásd: kontinuumhipotézis).
  • A \(\mathbb{W}\) halmaz nem kapható meg Cayley–Dickson konstrukcióval (más szóval nem kvaternion).
  • Ha a \((G; \oplus)\) csoport kommutatív (azaz Abel-csoport), és a \(G\) halmaz egységeleme a , akkor (és csakis akkor) a \((G; \oplus)\) csoportot Walter-csoportnak nevezzük.
  • Ebből következik, hogy \(W = (G, \oplus, \otimes)\) test Walter-test akkor és csakis akkor, ha \((G; \oplus)\) Walter-csoport, továbbá
  • a \(\mathcal{W} = (G, \oplus, \otimes)\) gyűrű Walter-gyűrű akkor és csakis akkor, ha \((G, \oplus)\) Walter-csoport.

1Feri nevét megváltoztattuk a pofonok elkerülése érdekében.

2Az én nevemet is megváltoztattuk.